Case 3.9
Conditions:
- Free running at model point in calm water (mandatory)
- With propeller, With rudder
- With bilge keels
- \( FR_{all} \)
- \( {R_{e}}^{*}=3.39 \times 10^6, {F_r}^{*}=0.20 \)
- \( L_{WL} = 3.147 \) [m], approach speed \(V_A = 1.11\) [m/s]
- Target Yaw angle: \(\psi_{C} = 0^{\circ} \)
- Rudder angle should be controlled in the following Computational Setup.
\( {R_{e}}^{*}\) : nominal Reynolds number, the Reynolds number when ship runs in calm water with constant propeller rate of revolution.
\( {F_r}^{*}\) : nominal Froude number, the Froude number when ship runs in calm water with constant propeller rate of revolution.
All quantities are non-dimensionalized by approach speed (\(V_A\)), and waterline length (\(L_{WL}\)):
\begin{align*}
F_r = \frac{V_A}{\sqrt{g \cdot L_{WL}}}, \quad R_e = \frac{V_A\ \cdot L_{WL}}{\nu}
\end{align*}
where \(g\) is the gravitational acceleration and \(\nu\) is the kinematic viscosity.
Computational Setup:
- All calculations are to be conducted for model scale conditions.
- All simulations results should be provided in the format described in next section.
- The propeller rate of revolution should correspond to the self propulsion point of the model (In case self-propulsion cannot be carried out, propeller rate of revolution should be set the measured value 8.97[rps]).
- Similar to the experiment, the rudders should be controlled by following autopilot:
\begin{align*}
\delta (t) = K_P ( \psi (t) - \psi_C )
\end{align*}
where \(\delta (t)\) is rudder angle, proportional gain \( K_P \) is 1.0, \(\psi_C\) is the target yaw angle and \(\psi(t)\) is yaw angle. The maximum rudder rate should be assigned to \(35.0\) [deg/s].
General Format for Submissions:
- Sinkage \(\sigma\), trim \(\tau\), velocity \(u\), propeller thrust coefficient \(K_T\) and torque coefficient \(K_Q\), propeller rate of revolution \(n\), resistance and its components \(C_{T(SP)}, C_{P(SP)}, C_{F(SP)}\) should be submitted.
- Sinkage \(\sigma\) should be given in an Earth-fixed coordinate system with \(z\) pointing downward as shown in Figure 1. Trim \(\tau\) is positive for bow up position. Sinkage should be normalized by \(L_{WL}\) and trim should be reported in degree.
-
The velocity \(u\) should be reported in ship-fixed coordinate system with \(x\) axis positive toward bow.
The reported velocities should be non-dimensionalized as \( u = \dot{x}\, / V_A \) .
- The propeller thrust \(T\) and torque \(Q\) should be reported in shaft coordinate system axis positive toward the engine. Values should be normalized by density of water\(\rho\), propeller diameter (\(D_P\)), and \(n\) as follows.
\begin{align*}
K_T = \frac{T}{ \rho n^2 {D_P}^4 }, \quad
K_Q = \frac{Q}{ \rho n^2 {D_P}^5 }
\end{align*}
-
Total resistance and its components \(C_{T(SP)}, C_{F(SP)}, C_{P(SP)}\) should be reported in ship coordinate system. They should be non-dimensionalized using wetted surface area at rest \(S_0\) and ship speed:
\begin{align*}
C_T = \frac{R_T}{ \frac{1}{2} \rho {V_A}^2 S_0 }, \quad
C_F = \frac{R_F}{ \frac{1}{2} \rho {V_A}^2 S_0 }, \quad
C_P = \frac{R_P}{ \frac{1}{2} \rho {V_A}^2 S_0 }, \quad
\end{align*}
- In case self-propulsion cannot be carried out, propeller rate of revolution should be set the measured value 8.97[rps] and \(T_x-R_T\) should be also reported where \(T_x\) is the propeller thrust in ship-fixed coordinate system.
- SI units should be used throughout (i.e. m, m/s, etc). Exceptions are angles in degrees.
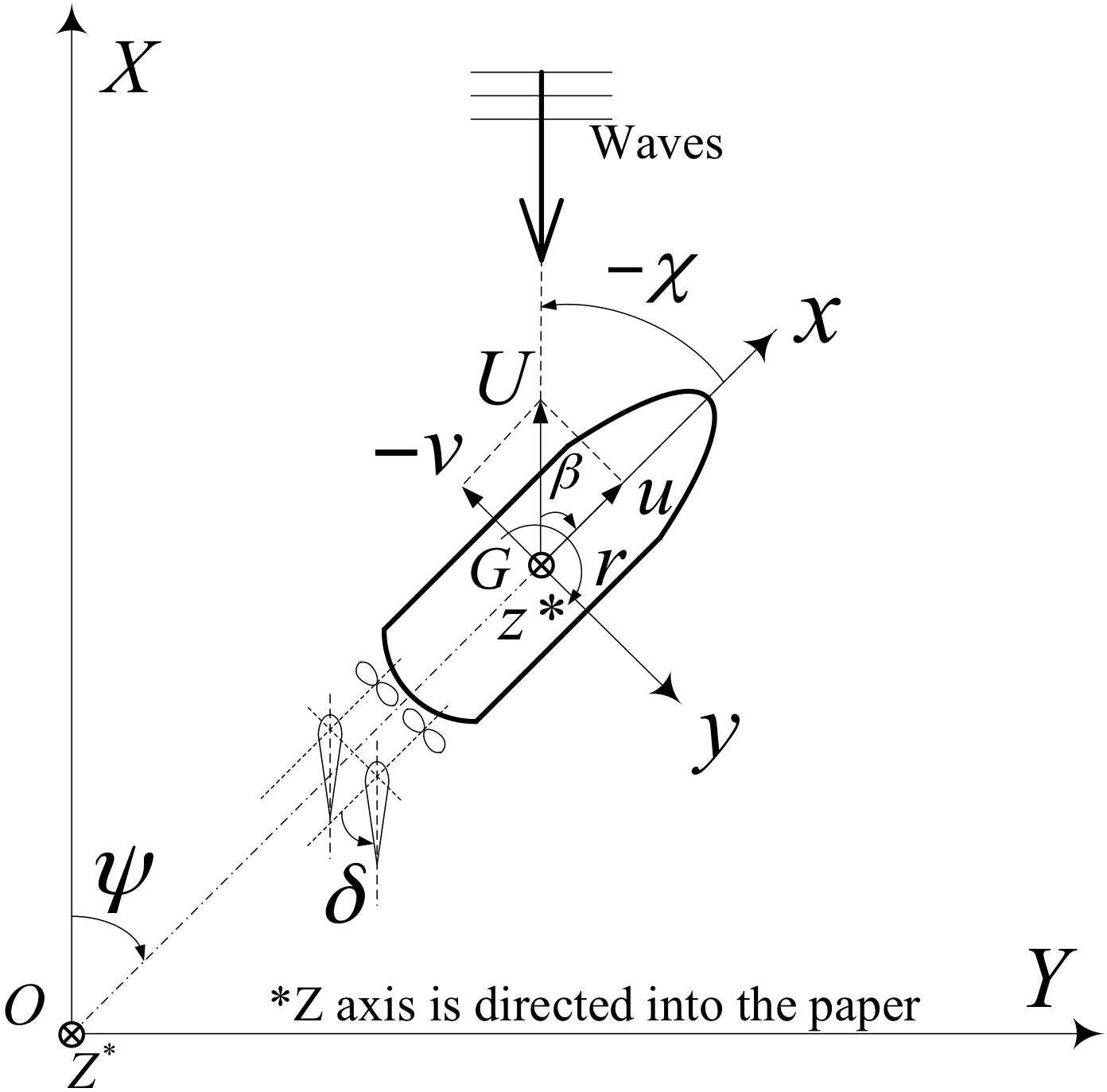
Figure 1: Earth and ship-fixed coordinate system
Submission Instructions:
- [Identifier] should be [Institute Name]-[Solver Name]. For example, if your institute is NMRI and solver is SURFv7, identifier should be NMRI-SURFv7.
- Identifier in the Figure should be [Institute Name]/[Solver Name]. For example, if your institute is NMRI and solver is SURFv7, identifier should be NMRI/SURFv7.
- All figures should be in black and white.
- Authors may change the contour levels for turbulence quantities for better qualitative comparison.
References:
Not yet available.
Details of EFD procedures are shown here (IIHR_ONRT_DATA_06-12-2015.pdf).
| Table/Figure#
| Items
| EFD Data
| Submission Instruction
|
| Data file |
Image |
Image files |
Sample + Tecplot layout file |
| 3.9-1 |
for \(\psi_C=0^{\circ}\) |
Ship motions
\(u\), sinkage and trim
|
Refer to sample file for detail |
N/A |
[Identifier]_Case3.9.xlsx |
| 3.9-2 |
Propulsion coefficients
\(K_T\), \(K_Q\), \(n\), \(C_{T(SP)}\), \(C_{F(SP)}\), \(C_{P(SP)}\) (and \(T_x - R_{T(SP)}\) (if \(n\) is set to the measured value and self-propulsion is not conducted) |
N/A |
N/A |
N/A |

