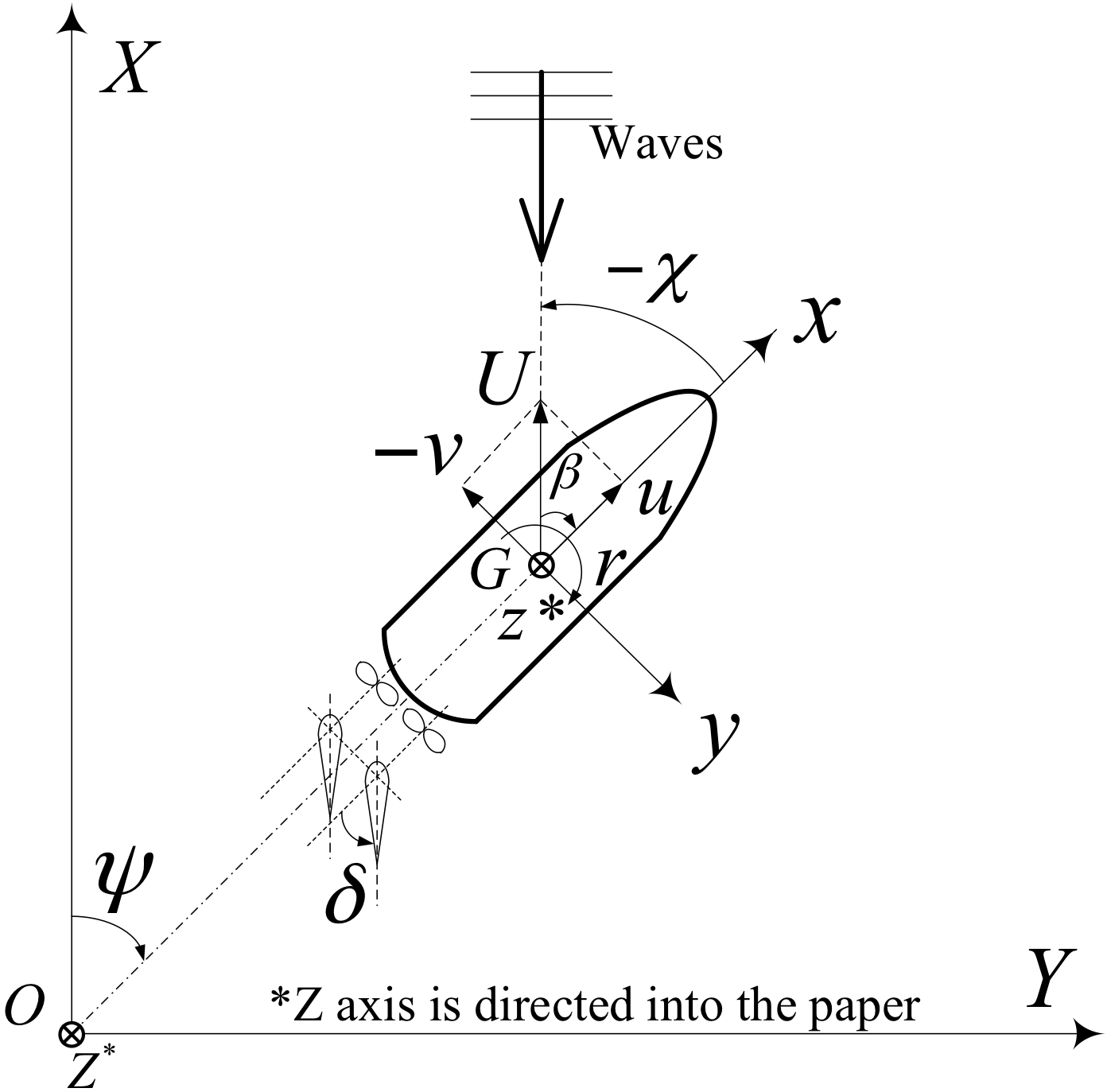
Figure 1: Earth and ship-fixed coordinate system
\( {R_{e}}^{*}\) : nominal Reynolds number, the Reynolds number when ship runs in calm water with constant propeller rate of revolution.
\( {F_r}^{*}\) : nominal Froude number, the Froude number when ship runs in calm water with constant propeller rate of revolution.
\(\lambda\) : wave length
\(H\) : wave height
\(\zeta_a\) : wave amplitude, \(\zeta_a = \displaystyle{\frac{H}{2}}\)
\(k\) : wave number, \(\displaystyle{k=\frac{2 \pi}{\lambda}}\)
All quantities are non-dimensionalized by approach speed (\(V_A\)), and waterline length (\(L_{WL}\)): \begin{align*} {F_r}^{*} = \frac{V_A}{\sqrt{g \cdot L_{WL}}}, \quad {R_e}^{*} = \frac{V_A\ \cdot L_{WL}}{\nu} \tag{1} \end{align*} where \(g\) is the gravitational acceleration and \(\nu\) is the kinematic viscosity.

Not yet available.
Details of EFD procedures are shown here (IIHR_ONRT_DATA_06-12-2015.pdf).
| Table/Figure# | Items | EFD Data | Submission Instruction | |||
|---|---|---|---|---|---|---|
| Data file | Image | Image files | Sample + Tecplot layout file | |||
| 3.12-1 | for \(\psi_C=0^{\circ}\) | Trajectory \(\displaystyle{\left(\frac{X-X_0}{L_{WL}}, \frac{Y-Y_0}{L_{WL}}\right)}\) Time histories of ship motions, rudder angle and wave elevation \(\displaystyle{\frac{Z}{\zeta_a}}\) \(\displaystyle{\frac{\phi}{k \zeta_a}}\), \(\displaystyle{\frac{\theta}{k \zeta_a}}\), \(\displaystyle{\frac{\psi-\psi_C}{k \zeta_a}}\), \(\displaystyle{u}\), \(\displaystyle{v}\), \(\displaystyle{w}\), \(\displaystyle{p}\), \(\displaystyle{q}\), \(\displaystyle{r}\), \(\displaystyle{\delta}\) and \(\displaystyle{\frac{\zeta_w}{L_{WL}}}\) |
Refer to sample file for detail |
Filename: [Identifier]_XY_3-12.png ( for Trajectory ) [Identifier]_heave_T-his_3-12.png ( for \(Z/\zeta_a\) ) [Identifier]_roll_T-his_3-12.png ( for \(\phi/(k \zeta_a)\) ) [Identifier]_pitch_T-his_3-12.png ( for \(\theta/(k \zeta_a)\) ) [Identifier]_yawdvtn_T-his_3-12.png ( for \((\psi-\psi_C)/(k \zeta_a)\) ) [Identifier]_u_T-his_3-12.png ( for \(u\) ) [Identifier]_v_T-his_3-12.png ( for \(v\) ) [Identifier]_w_T-his_3-12.png ( for \(w\) ) [Identifier]_p_T-his_3-12.png ( for \(p\) ) [Identifier]_q_T-his_3-12.png ( for \(q\) ) [Identifier]_r_T-his_3-12.png ( for \(r\) ) [Identifier]_rudder_T-his_3-12.png ( for \(\delta\) ) [Identifier]_wave_T-his_3-12.png ( for \(\zeta_w/L_{WL}\) ) X-axis range:
Y-axis range:
Style: CFD solid line EFD open circles Time interval of EFD data: \(\Delta t = 0.2 \)[s](4 skips), for trajectory \(\Delta t = 0.4 \)[s](8 skips), for time histories of \(\phi/(k \zeta_a)\), \((\psi - \psi_C)/(k \zeta_a), p, r\) and \(\delta\) \(\Delta t = 0.2 \)[s](4 skips), for time histories of \(v\) \(\Delta t = 0.1 \)[s](2 skips), for time histories of \(u\) \(\Delta t = 0.05 \)[s], for time histories of the others |
Case3.12-000.zip | |
| 3.12-2 | Time histories of propulsion coefficients \(K_T\), \(K_Q\) and \(n\) |
N/A | N/A |
Filename: [Identifier]_KT_T-his_3-12.png ( for \(K_T\)) [Identifier]_10KQ_T-his_3-12.png ( for \(10 K_Q\)) [Identifier]_n_T-his_3-12.png ( for \(n\)) X-axis range: \( \displaystyle{ 0.0 \le \frac{(t-t_0) V_A}{L_{WL}} \le 10.0 }\) Y-axis range: \( 0.1 \le K_T \le 0.6\) \( 0.4 \le 10 K_Q \le 1.2\) \( 8.0 \le n \le 10.0\) Style: Port side solid line Starboard side dashed line |
||