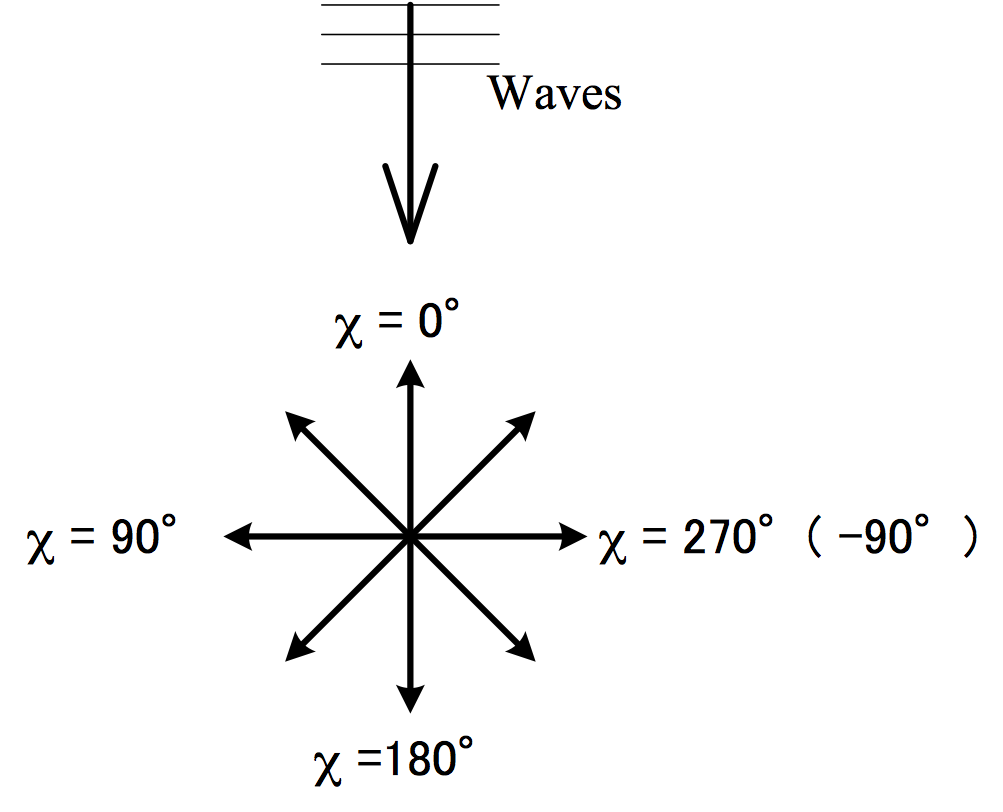
Figure 1: Relationship between ship heading and wave encounter angle. (Arrow shows ship heading)
| No. | C0 | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|---|
| Speed [m/s] | \(1.34\) | |||||
| Froude number (\(F_r\)) | 0.26 | |||||
| Reynolds number (\(R_e\)) | \(3.738 \times 10^6\) | |||||
| Wave encounter angle: \(\chi\) [deg] | Calm water | 0(head sea) | 45(bow sea) | 90(beam sea) | 135(quartering sea) | 180(following sea) |
| Wave length: \(\lambda\) [m] | 2.7 | |||||
| Wave height: \(H_s\) [m] | 0.045 | |||||
\(\zeta_s\) : wave amplitude, \(\zeta_s = \displaystyle{\frac{H_s}{2}}\)
\(k\) : wave number, \(\displaystyle{k=\frac{2 \pi}{\lambda}}\)
Note: The surge, heave, roll and pitch motions are given at center of gravity. The wave crest is at FP when \(t = 0\).
EFD data was taken by surge free mount system (mass-spring-damper system). Parameter setting of surge free mount is as follows:
Surge fixed computation is recommended for participants.
Spring constant (K)
100 [N/m]
Damper coefficient (D)
10 [N/(m/s)]
Not yet available.
| Table/Figure# | Items | EFD Data | Submission Instruction | ||
|---|---|---|---|---|---|
| Data file | Image | Image files | Sample + Tecplot layout file | ||
| 2.11-1 | Comparison of:
<in head waves> |
Refer to sample file for details | Filename: |
[Identifier]_6conditions_2-11_20151112.xlsx (updated on November, 13, 2015) |
|
| 2.11-2-C1 | Time histories of total resistance coefficient (\(C_T\)), surge motion (\(x/\zeta_s\)), heave motion (\(z/\zeta_s\)), roll motion(\(\phi/ k \zeta_s\)) and pitch angle (\(\theta/ k \zeta_s\)), which are reconstructed from the Fourier Series (not the raw signals) (test condition 1) |
Refer to sample file for details | Filename: [Identifier]_CT_T-his_C1_2-11.png ( for \(C_T\) ) [Identifier]_surge_T-his_C1_2-11.png ( for \(x/\zeta_s\) ) [Identifier]_heave_T-his_C1_2-11.png ( for \(z/\zeta_s\) ) [Identifier]_roll_T-his_C1_2-11.png ( for \(\phi/ k \zeta_s\) ) [Identifier]_pitch_T-his_C1_2-11.png ( for \(\theta/ k \zeta_s\) ) X-axis range: \( 0.0 \le t / T_e \le 1.0 \) Y-axis range: \( 0.0066 \le C_T \le 0.0071 \) \(-0.03 \le \displaystyle{\frac{x }{\zeta}} \le 0.12 \) \(-1.0 \le \displaystyle{\frac{z }{\zeta}} \le 1.0 \) \(-0.4 \le \displaystyle{\frac{\phi }{k \zeta}} \le 0.4 \) \(-0.8 \le \displaystyle{\frac{\theta}{k \zeta}} \le 0.8 \) Style: CFD solid line EFD open circles |
Case2.11-2_20151112.zip (updated on November, 13, 2015) |
|
| 2.11-2-C2 | Time histories of total resistance coefficient (\(C_T\)), surge motion (\(x/\zeta_s\)), heave motion (\(z/\zeta_s\)), roll motion(\(\phi/ k \zeta_s\)) and pitch angle (\(\theta/ k \zeta_s\)), which are reconstructed from the Fourier Series (not the raw signals) (test condition 2) |
Refer to sample file for details | Filename: [Identifier]_CT_T-his_C2_2-11.png ( for \(C_T\) ) [Identifier]_surge_T-his_C2_2-11.png ( for \(x/\zeta_s\) ) [Identifier]_heave_T-his_C2_2-11.png ( for \(z/\zeta_s\) ) [Identifier]_roll-his_C2_2-11.png ( for \(\phi/ k \zeta_s\) ) [Identifier]_pitch_T-his_C2_2-11.png ( for \(\theta/ k \zeta_s\) ) X-axis range: \( 0.0 \le t / T_e \le 1.0 \) Y-axis range: \( 0.0058 \le C_T \le 0.0068 \) \(-0.15 \le \displaystyle{\frac{x }{\zeta}} \le 0.20 \) \(-1.5 \le \displaystyle{\frac{z }{\zeta}} \le 1.5 \) \(-1.6 \le \displaystyle{\frac{\phi }{k \zeta}} \le 0.8 \) \(-0.8 \le \displaystyle{\frac{\theta}{k \zeta}} \le 0.8 \) Style: CFD solid line EFD open circles |
||
| 2.11-2-C3 | Time histories of total resistance coefficient (\(C_T\)), surge motion (\(x/\zeta_s\)), heave motion (\(z/\zeta_s\)), roll motion(\(\phi/ k \zeta_s\)) and pitch angle (\(\theta/ k \zeta_s\)), which are reconstructed from the Fourier Series (not the raw signals) (test condition 3) |
Refer to sample file for details | Filename: [Identifier]_CT_T-his_C3_2-11.png ( for \(C_T\) ) [Identifier]_surge_T-his_C3_2-11.png ( for \(x/\zeta_s\) ) [Identifier]_heave_T-his_C3_2-11.png ( for \(z/\zeta_s\) ) [Identifier]_roll_T-his_C3_2-11.png ( for \(\phi/ k \zeta_s\) ) [Identifier]_pitch_T-his_C3_2-11.png ( for \(\theta/ k \zeta_s\) ) X-axis range: \( 0.0 \le t / T_e \le 1.0 \) Y-axis range: \( 0.0 \le C_T \le 0.008 \) \(-0.1 \le \displaystyle{\frac{x }{\zeta}} \le 0.1 \) \(-1.5 \le \displaystyle{\frac{z }{\zeta}} \le 1.5 \) \(-1.2 \le \displaystyle{\frac{\phi }{k \zeta}} \le 1.2 \) \(-0.15 \le \displaystyle{\frac{\theta}{k \zeta}} \le 0.15 \) Style: CFD solid line EFD open circles |
||
| 2.11-2-C4 | Time histories of total resistance coefficient (\(C_T\)), surge motion (\(x/\zeta_s\)), heave motion (\(z/\zeta_s\)), roll motion(\(\phi/ k \zeta_s\)) and pitch angle (\(\theta/ k \zeta_s\)), which are reconstructed from the Fourier Series (not the raw signals) (test condition 4) |
Refer to sample file for details | Filename: [Identifier]_CT_T-his_C4_2-11.png ( for \(C_T\) ) [Identifier]_surge_T-his_C4_2-11.png ( for \(x/\zeta_s\) ) [Identifier]_heave_T-his_C4_2-11.png ( for \(z/\zeta_s\) ) [Identifier]_roll_T-his_C4_2-11.png ( for \(\phi/ k \zeta_s\) ) [Identifier]_pitch_T-his_C4_2-11.png ( for \(\theta/ k \zeta_s\) ) X-axis range: \( 0.0 \le t / T_e \le 1.0 \) Y-axis range: \( 0.001 \le C_T \le 0.007 \) \(-0.8 \le \displaystyle{\frac{x }{\zeta}} \le 0.8 \) \(-0.8 \le \displaystyle{\frac{z }{\zeta}} \le 0.8 \) \(-4.5 \le \displaystyle{\frac{\phi }{k \zeta}} \le 4.5 \) \(-0.8 \le \displaystyle{\frac{\theta}{k \zeta}} \le 0.8 \) Style: CFD solid line EFD open circles |
||
| 2.11-2-C5 | Time histories of total resistance coefficient (\(C_T\)), surge motion (\(x/\zeta_s\)), heave motion (\(z/\zeta_s\)), roll motion(\(\phi/ k \zeta_s\)) and pitch angle (\(\theta/ k \zeta_s\)), which are reconstructed from the Fourier Series (not the raw signals) (test condition 5) |
Refer to sample file for details | Filename: [Identifier]_CT_T-his_C5_2-11.png ( for \(C_T\) ) [Identifier]_surge_T-his_C5_2-11.png ( for \(x/\zeta_s\) ) [Identifier]_heave_T-his_C5_2-11.png ( for \(z/\zeta_s\) ) [Identifier]_roll_T-his_C5_2-11.png ( for \(\phi/ k \zeta_s\) ) [Identifier]_pitch_T-his_C5_2-11.png ( for \(\theta/ k \zeta_s\) ) X-axis range: \( 0.0 \le t / T_e \le 1.0 \) Y-axis range: \( 0.0030 \le C_T \le 0.0055 \) \(-0.4 \le \displaystyle{\frac{x }{\zeta}} \le 0.4 \) \(-0.5 \le \displaystyle{\frac{z }{\zeta}} \le 0.3 \) \(-0.4 \le \displaystyle{\frac{\phi }{k \zeta}} \le 0.2 \) \(-0.5 \le \displaystyle{\frac{\theta}{k \zeta}} \le 0.5 \) Style: CFD solid line EFD open circles |
||
Note:
a positive (+) surge(x) value is defined forward and a positive (+) heave (z) value is defined upwards.
a positive (+) roll(\(\phi\)) value is portside up and positive (+) pitch (\(\theta\)) value is defined bow up.
Submission Instructions:
All quantities are non-dimensionalized by denstiy of water (\(\rho\)), ship speed (\(U\)), and length between parpendiculars (\(L_{PP}\)): \begin{align*} F_r = \frac{U}{\sqrt{g \cdot L_{PP}}}, \quad R_e = \frac{U \cdot L_{PP}}{\nu} \tag{1} \end{align*} where \(g\) is the gravitational acceleration and \(\nu\) is the kinematic viscosity.

As a time reference, incident wave height at FP of the ship is defined as
\begin{align*}
\zeta_T (t) = \frac{\zeta_s}{L_{PP}} \cos ( 2 \pi f_e t + \gamma_I ) \tag{3}
\end{align*}
\(\gamma_I\) is the initial phase and is equal to be zero from the present definition of \(t=0\) below.
Fourier series for time history \(X\) (\(X=C_T\), \(x\), \(z\), \(\phi\), \(\theta\), and \(\zeta_T\)) are determined as follows:
\begin{align*}
X_F (t) &= \frac{X_0}{2} + \sum_{n=1}^N X_n \cos ( 2 n \pi f_e t + \Delta \gamma_n ) \tag{4} \\
\Delta \gamma_n &= \gamma_n - \gamma_I \tag{5}\\
a_n &= \frac{2}{T_e} \int_0^{T_e} X(t) \cos ( 2 n \pi f_e t ) dt \quad ( n = 0, 1, 2, \cdots ) \tag{6} \\
b_n &= \frac{2}{T_e} \int_0^{T_e} X(t) \sin ( 2 n \pi f_e t ) dt \quad ( n = 1, 2, \cdots ) \tag{7} \\
X_n &= \sqrt{ {a_n}^2 + {b_n}^2 } \tag{8} \\
\gamma_n &= tan^{-1} \left( - \frac{b_n}{a_n} \right) \tag{9}
\end{align*}
\(X_n\) is n-th harmonic amplitude and \(\gamma_I\) is the corresponding phase.